一、1815曾彦翔解题:


二、1815皮家齐解题:


1815皮家齐的解题思路及方法:
第(1)小题是一个简单的三角形中求角度问题,只需要作垂线利用30°直角三角形性质即可解出。
第(2)小题略有难度,发现其中的弦中点得垂直,得到四点共圆后基本便完成了。
第(3)小题题干中出现了三角形面积的平方之差,考虑到这两个欲求面积的三角形均有一个角为定值,且该角所夹的两边对应均存在勾股定理关系式,因此考虑设出基本边,用其去表示这两个三角形面积的平方差化简即可得到第一个关系式。同时结合余弦定理(即为前部分引理所证明的(*)式)可得到另一个关系式。利用这两个式子即可解出本题。
三、1815唐自远解题:

1815班唐自远的解题思路及方法:
将角CAB设为θ,利用三角恒等变形化简题目中已知的关系式,再结合余弦定理将AC用含θ的式子表示并求值即可
四、1815谭阳鸿解题:

1815谭阳鸿的解题思路及方法:

五、1815唐乾程解题:

1815唐乾程的解题思路及方法:
先根据题目条件S1平方—S2平方=21,利用平方差求出求出△ACB的面积,从而由正弦定理得出 CD与CE的乘积,再利用正弦定理(S△ODE)、托勒密定理(⊙ODCE)、勾股定理(Rt△OCE)找出 CD、CE、OD、OE关系,最后解四元二次方程即可。
六、1815杨雪健解题:

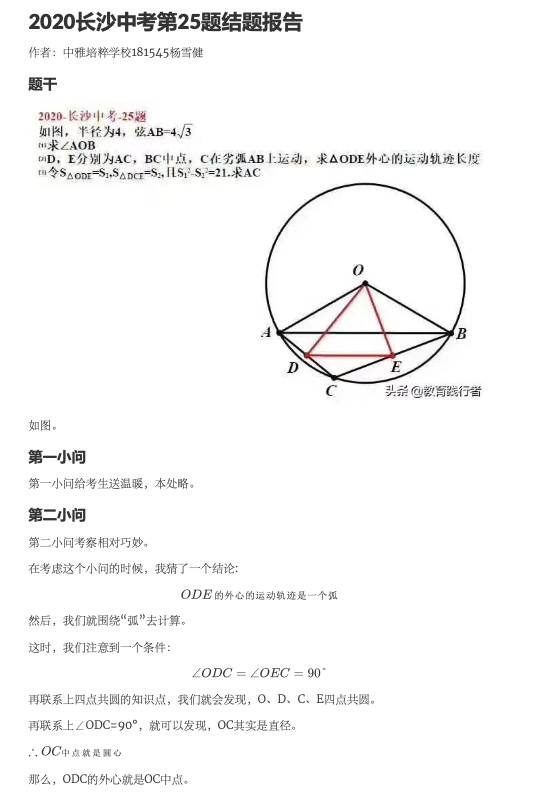

七、1815李颐解题:

1815李颐的解题思路及方法:
(1)正弦定理,解三角形均可。
(2)有等腰,中点可出直角,发现O、D、E、C四点共圆。
(3)S1、S2若直接用AC、BC表示,会过于复杂,先试探隐蔽的关系,与条件联立,求出后,设出AC,BC结合三角形面积公式S=1/2absinC及OE、OD、CD、CE与OC之间的勾股关系列出方程即可。
八、1815肖佳成解题:

肖佳成的思路及方法:
利用三角形中位线,运用圆的解析式求出点的坐标,最后用两点之间距离公式计算。处理题目给出的式子时,用平方差公式展开,观察在图中的几何意义,利用等量关系设出a,b求解即可
九、1815陈胤锦解题:

1815陈胤锦的解题思路及方法:
遇到这种角度关系少,图并不复杂,且一般有直角的题目可以考虑解析法。不妨在圆心建系,由前面的计算可以容易得到A,B的坐标。参考圆在坐标系中的方程,又可以设出C的横坐标m并表示C的纵坐标。联系向量叉积的几何意义,可以很方便地计算出三角形的面积并写出S1和S2。利用平方差公式并结合题目中S1^2-S2^2=21,可以带入并解得m的值,最后得出C的坐标并用距离公式算出AC的值即可。
十、1815陈传玺解题:


1815陈传玺的解题思路和分析:
首先,题目中给了两个三角形的面积平方的差,所以在图上找出这两个三角形,会发现,这两个三角形正好同底,且底已知,所以我们可以把它简化一下。
用底乘高表示,所以做了两条垂线,顺便把MN给约掉。就只剩下OF^2-CD^2=21
又因为OF=0E+EF,还有一条中位线,可以得到CD=EF,所以就很容易就把CD和EF求出来,等于3/4。
然后观察要求的AC,想和CD直接联系算出来,就得求MD的值,但想不做辅助线,就必须暴算。(我算过了,比较恶心,不建议)所以我们可以把条件转化一下,图上正好有关AC,CD,并且还大部分已知的就是三角形CMD和三角形MOF两个三角形相似,所以要求FN,所以就想到连EN证全等。再用相似三角形边之间的比例关系列方程,就可以求出AC。
十一、1804胡小宇解题:

1804胡小宇的解题思路和分析:
(1)根据题目已知条件:半径为4,弦AB为四倍根号三,所以用垂径定理,可以算出三角形AOZ为30度,60度的直角三角形,所以可以求出角AOB=120度。
(2)第二问求三角形ODE的外心,因为点C在线段AB上运动,我们可以知道外心在以O为圆心,AO的一半为半径的圆上运动,所以可以求出三角形ODE外心的运动轨迹的长度为4/3倍根号三。
(3)第三问求线段AC的长度,很容易可以想到把点的坐标表示出来用公式求线段长,于是便可以O为圆心,建立平面直角坐标系,所以圆O的方程为x^2+y^2等于16,然后将点C的坐标设出来,又因为点D和多E分别是线段AC,线段BC的中点,可以表示出点D和点E的坐标,又由题目可知s1方减掉s2方等于21,所以我们可以求出(l1+l2)×(l1-l2)等于七,然后可以算出点C的坐标为(二分之根号15,-7/2)或(二分之根号15,-7/2)通过点A的坐标,我们可以求出AC的长度为 根号三加根号15或根号15减根号三。
十二、1815霍盾解题:

1815霍盾的解题思路和方法:
第一小问较简单,很明显是根据直角三角形三边关系求角度,只需做垂直即可。
第二小问中题目隐藏了垂直这一信息,但只要稍作分析就可以发现,进而得到四点共圆
第三小问中出现两个三角形面积的平方差,而三角形的底易知,则考虑作高,再结合三角形的中位线列方程便可求出高的值。圆中常见辅助线中有一条是连半径,不妨连接OC,这时我们会十分幸运地得到一对相似三角形,并能根据已知条件求出各个线段的长,最后根据勾股定理求出AC。
总的来说,第三问的精髓在作高,中位线,连半径。有机结合三角形面积,相似三角形,以及勾股定理。
最后要注意的是圆的对称性,不要漏掉另一个答案。
(由1815谭阳鸿整理)
